Úloha 8.1 Určete vzdálenost dvojhvězdy, známe-li její oběžnou dobu
|
Úloha 8.1 Určete vzdálenost dvojhvězdy, známe-li její oběžnou dobu
|
|
Úloha 8.2 Můžeme pomocí Hubbleova dalekohledu rozlišit dvě hvězdy spektrální třídy O, mezi kterými je úhel
|
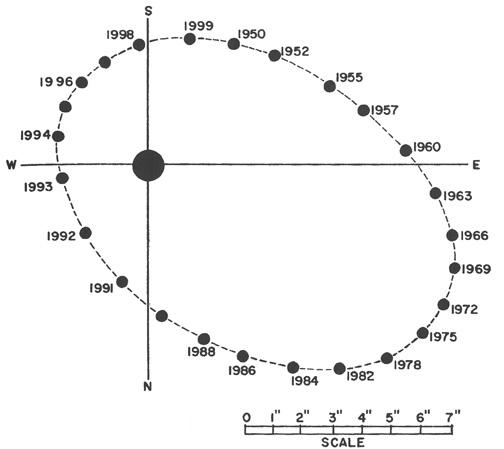
Pozorované dráhy Síria A a B
|
Úloha 8.5 Fyzická dvojhvězda 2MASSWJ0746425+2000321, se skládá z červeného a hnědého trpaslíka. Z pozorování byla zjištěna oběžná doba
|
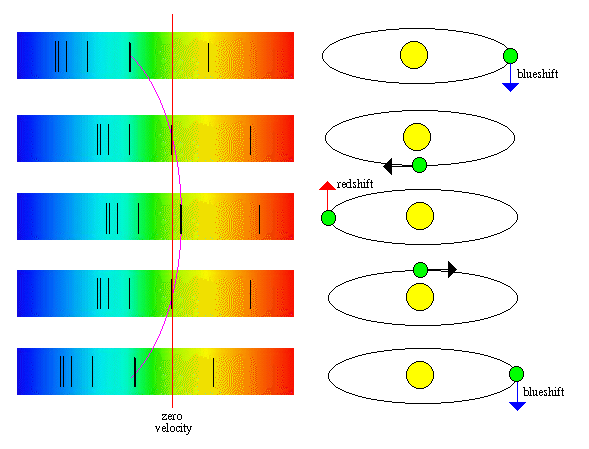
Spektroskopická dvojvězda
|
Úloha 8.13 Dokažte, že pro relativní změnu oběžné doby dvojhvězdy s přenosem hmoty platí
|
|
Úloha 8.14 Dokažte, že u těsných dvojhvězd je časová změna oběžné doby způsobená přenosem hmoty dána vztahem
|
|
Úloha 8.16 U dvojhvězdné soustavy s hmotnostmi jednotlivých složek
|
|
|
|
Úloha 8.22Neutronovou hvězdu - pulsar s hmotností
|